LEAD: Min-Max Optimization from a Physical Perspective
The development of efficient optimization methods for games is an active area of research with a timely impact on adversarial formulations including GANs. Existing methods for this type of problem typically employ intuitive, carefully hand-designed mechanisms for controlling the problematic rotational dynamics commonly encountered during optimization. In this work, we cast min-max optimization as a physical system. We propose LEAD (Least-Action Dynamics), an optimizer that uses the principle of least-action from physics to discover an efficient optimizer. We provide convergence analysis and showcase its superiority in GAN training.
Warm Up!
To begin, let us first take note of a central principle governing the physical world around us, namely the principle of least action (or more generally stationary action).
The principle states that the movement of physical systems, from the falling of a ball to the motion of electrons in an atom, is guided by an entity called the action (\( A\)). Specifically, the trajectory of motion of such natural systems is such that it minimizes (or extremizes) \( A\). To exemplify this point, let us consider a visual example! Think of Newton throwing an apple in the air. We know that the apple does not just take any random path to reach the ground,
Rather the apple follows a specific projectile motion,
Incidentally, as it can be easily checked, the principle of least action applied in this context states that the trajectory of the apple is given by the solution of the equation,
$$\vec{F}_{gravity} = m \ a,$$
where \( F_{gravity} \) is the (downwards) gravitational force acting on the apple, \(m \) is the mass of the apple and \(a \) its acceleration. This equation is commonly known as Newton’s 2nd Law, and can be interpreted as the trajectory of motion of a physical system under a force F, as outlined by the least action principle.
From Physics to Optimization
Now, to bring to light how the dynamics of physical systems such as that of the apple above, can be connect with machine learning optimization, we note that for conservative forces Newton’s 2nd Law takes the form,
$$ - \nabla f(x) = m \ddot{x}, $$
where \(f(x) \) is the loss function. Although this equation might seem unfamiliar, it is the continuous-time dynamics of a popular optimization algorithm in machine learning, i.e., gradient descent with momentum.
Taking inspiration from this, in the following, we set out to determine a corresponding physical system which can provide an efficient optimizer in the context of two-player zero-sum games!
Games
Multi-objective or game optimization is a common ML formulation observed in GANs, multi-task learning, and multiagent settings in RL. In this work, we aim to tackle the following min-max zero-sum game,
$$ \min_x \max_y f(x, y),$$
where \(f(x,y)\) is the loss function and player one only controls \(x\) and player two only controls \(y\).
It has been observed that gradient descent-ascent performs poorly in game optimization. Specifically, we observe rotational dynamics around the Equilibrium point of the game, which slows down convergence. A simple example of the above formulation is the bilinear game where \(f(x, y) = xy \) . The bilinear game has been extensively studied in literature as it allows us to study game optimization in a simple setup. At the same time, it shares many of the properties of more complex systems. In this game, gradient descent ascent follows,
$$ x_{k+1} = x_k - \eta \nabla_x f(x_k, y_k) = x_k - \eta y_k$$ $$ y_{k+1} = y_k + \eta \nabla_y f(x_{k}, y_k) = y_k + \eta x_{k}$$
If we start somewhere around the Equilibrium point of this game (in this case \((0, 0)\)), the players will slowly diverge away from the Equilibrium. This problem has also been observed in GAN optimization [1].
In the next section, we design a physical system that mimics game optimization properties and proposes mitigation based on the physical system to tackle the rotational dynamics.
The mechanics of Games
In order to model game optimization as a physical system, we need to model the dynamics of a particle in a 2-D plane that has the following equations of motion,
$$\ddot{x} = -\nabla_x f(x,y)$$ $$\ddot{y} = \nabla_y f(x,y)$$
The first extension that would naturally come to mind is to model these dynamics similar to gradient descent with momentum. However, in that case, we need a single potential function (\(f(x, y)\)) which is simultaneously positive and negative. Now we know that this is impossible. To understand this in more details, see this excellent blog post on how two-player games are non-conservative dynamical systems.
So the question persists, how can we model game dynamics as a physical system? Let's think about the properties of this system. We know that this system has rotational dynamics and diverges away from the optimum. One similar force in nature is the vortex force,
$$m \ddot{x} = F_{vortex} = -\nabla_x f(x,y)$$ $$m \ddot{y} = F_{vortex} = \nabla_y f(x,y)$$
On discretization, the above dynamics diverge in a bilinear game. This is in line with our observation of divergence of gradient descent-ascent with positive momentum in the bilinear games. So the vortex force does provide the main properties of the dynamics of gradient descent-ascent.
Now we can easliy modify the dynamics by introducing new forces to the system. What we need is a counteracting force to curb the rotations. One of such is the magnetic force,
$$ m \ \ddot{x} = F_{vortex} + F_{magnetic} = -\nabla_x f(x,y) -2q(\nabla_{xy} f)\dot{y}$$ $$ m \ \ddot{y} = F_{vortex} + F_{magnetic} = \nabla_y f(x,y) 2q(\nabla_{xy} f)\dot{x}$$
where \(q\) is the charge of the particle.
The plot on the left shows that the magnetic force has curbed the dynamics towards the inside, but still, it's not enough for convergence. This is predictable from a physics perspective. The vortex force is known to increase the particle's speed over time[2], while the magnetic force is known not to cause any change to the speed of the particle. Hence, under the influence of simply the curl and magnetic forces, our particle will keep increasing in velocity over time, preventing it from convergence.
The last piece is to add some form of dissipation to decrease the velocity of the particle. So we introduce friction to the system,
$$ m \ \ddot{x} = F_{vortex} + F_{magnetic} + F_{friction} = -\nabla_x f(x,y) -2q(\nabla_{xy} f)\dot{y} - \mu \dot{x}$$ $$ m \ \ddot{y} = F_{vortex} + F_{magnetic} + F_{friction} = \nabla_y f(x,y) + 2q(\nabla_{xy} f)\dot{x} - \mu \dot{y} $$
where \(\mu\) is the friction coefficient. This time we see that the friction causes the particle to lose speed and converge! You can play with the interactive plot above to see the effect of the friction and magnetic forces.
LEAD
In the previous section, we modeled game optimization as a physical system for a bilinear problem. Using the Least Action Principle and Newton's 2nd law, we derived the particle's equations of motion in continuous time. However, in machine learning, we need discrete-time algorithms. We can use a combination of explicit and implicit Euler method to discretize the system with all the forces,
$$x_{k + 1} = x_k + \beta (x_k - x_{k-1}) - \eta \nabla_{x} f(x_k, y_k) - \alpha \nabla_{xy}f(x_k, y_k) (y_k - y_{k-1}) $$ $$y_{k + 1} = y_k + \beta (y_k - y_{k-1}) + \eta \nabla_{y} f(x_k, y_k) + \alpha \nabla_{xy}f(x_k, y_k) (x_k - x_{k-1}) $$
where \(\delta \) is the discretization step and \(\alpha = 2 {q} \delta, \beta = 1 - {\mu} \delta, \eta = {\delta}^2 \) are hyper-parameters dependent on \(\mu, q\) and \(\delta\). We refer to the above update rule as Least Action Dynamics (LEAD).
We theoretically study LEAD on the bilinear game and prove exponential (linear) convergence rate for continuous and discrete-time dynamics. You can check the details of the Lyapunov and Spectral Analysis in the paper.
From Bilinear Games to GANs
A natural next step for us is to validate this method in GANs. It is important to note that although the term \(\nabla_{xy}f(x_k, y_k)\) is second order, we do not need to compute it. Using auto-differentiable tools such as PyTorch and Tensorflow, \(\nabla_{xy}f(x_k, y_k) (y_k - y_{k-1}) \) can be computed directly with the cost of computing two gradients. So computationally, our method is exactly equivalent to extra-gradient on a large scale.
To move to GAN experiments, we took two steps. First, we implemented LEAD on top of ADAM, an adaptive optimizer commonly used in machine learning. Next, we test our method in a ResNet architecture. Our method obtains a competitive FID score of 10.49 and an inception score of 8.82. See Table below for comparison with several other methods,
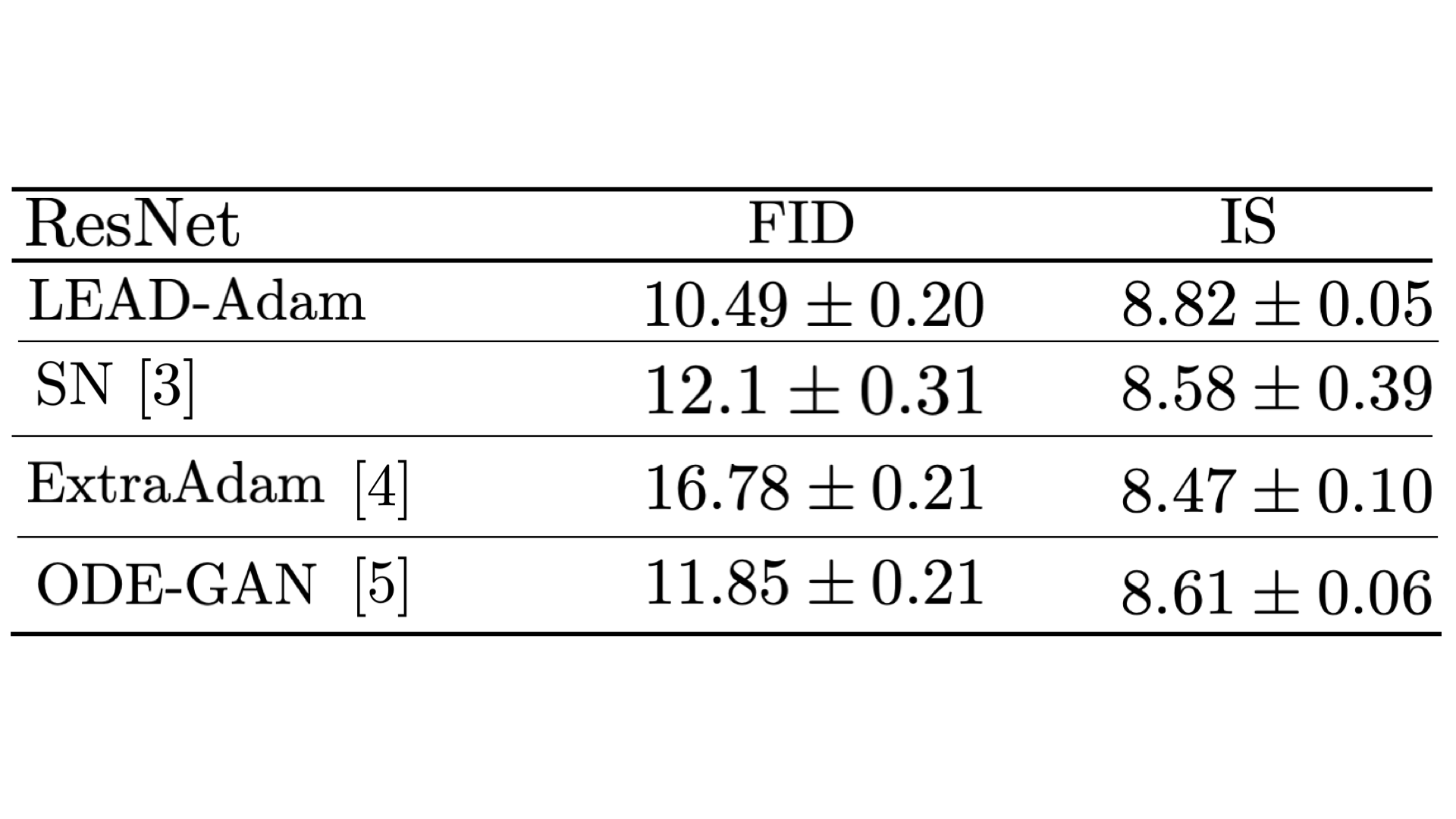
We compare in terms of both the FID and the inception score. Lower FID (or higher Inception Score), correspond to better sample quality. We have done other expirements and comparison with other methods that you can check their details in the paper.
Conclusion
In this work, we leverage tools from physics to propose a novel second-order optimization scheme LEAD, to address the issue of rotational dynamics in min-max games. Our analysis underlines the advantages of physical approaches in designing novel optimization algorithms for games as well as for traditional optimization tasks.
It is important to note in this regard that our crafted physical system is a way to model min-max optimization physically. Alternate schemes to perform such modeling can involve other choices of counter-rotational and dissipative forces which can be explored in future work.